Current Research Projects

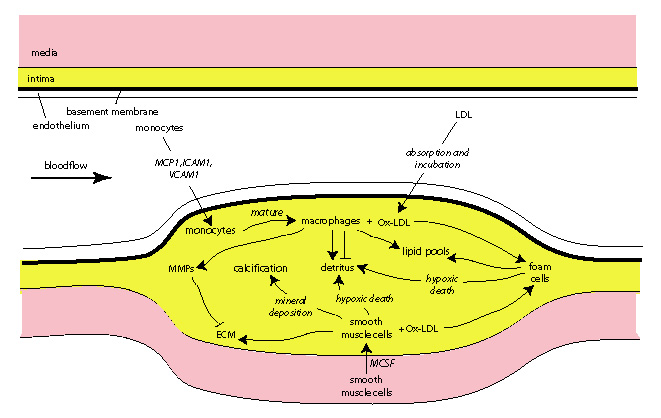
Cardiovascular disease (CVD) affected about 80 million Americans in 2006 and was responsible for 800,000 deaths. One common form of CVD is atherosclerosis which is a ``furring'' of the artery walls leading to a narrowing of the vessel lumen. It was originally thought that plaque build-up would make patients more susceptible to Myocardial Infarction (MI) or heart attacks. However, doctors now think that the rupture of certain plaques called Thin Capped Fibroatheromas or ''vulnerable plaques'' are responsible for most fatalities. In one study, 73% of all deaths from MI were caused by plaque rupture. This has led to the definition and characterization of vulnerable plaque which is thought to be the major culprit behind MIs.

The formation of plaque is a very complicated process. Some of the important factors are shown in the figure above. Our group is trying to quantify plaque growth in order to aid in the detection and diagnosis of plaque. Our research aims to answer some important basic questions concerning plaque growth. For example, how do shear stresses affect the leukocyte adhesion cascade (LAC) and, subsequently, how does the LAC affect plaque formation? Which factors determine whether a plaque remodels inwardly or outwardly? Why do necrotic cores form inside vulnerable plaques and what determines their shape?

Some relevant literature

1. The Vulnerable Atherosclerotic Plaque: Strategies for diagnosis and management, edited by R. Virmani, J. Narula, M. B. Leon, and J. T. Willerson. Blackwell 2007.
2. Shah, P. K., Mechanisms of Plaque Vulnerability and Rupture, Journal of the American College of Cardiology 41, No. 4 (2003).
3. Virmani et al., Lessons from sudden coronary death: A comprehensive morphological classification scheme for atherosclerotic lesions. Arteriosclerosis, Thrombosis and Vascular Biology 20 pp 1262-1275 (2000).
4. T. I. Zohdi, G. A. Holzapfel and S. A. Berger, A phenomenological model for atherosclerotic plaque growth and rupture. Journal of Theoretical Biology 227 pp 437-443 (2004).

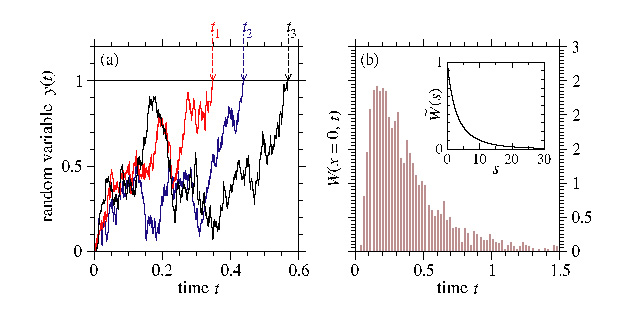
The study of stochastic processes is important in many branches of mathematics, science and engineering. One example of a stochastic process is a (persistant) brownian motion where changes in a walker's position arise from two components: a deterministic drift and a random noise. Now consider a situation where one only has knowledge of the exit times of a random walk, i.e. one only knows the times at which the random walker reaches a certain value. Is it possible to infer the drift from these times? This problem is a simple example of a Stochastic Inverse Problem . Such problems have great importance in biology. For example, under certain modeling assumptions, they can be used to interpret Dynamic Force Spectroscopy (DFS) data in the context of protein folding and chemical bond rupture.

In DFS experiments, an Atomic Force Microscope is used to slowly unfold a macromolecule. Because thermal fluctuations are important at such small scales, the data generated by such experiments consists not of a single rupture force, but a distribution of such forces. One active area of research is to interpret these data sets. What can the distribution of rupture forces tell us about how macromolecules fold and unfold?

The extent to which a macromolecule has unfolded can be described in terms its bond coordinate which, qualitatively, can be thought of as a measure of its end-to-end distance. Often, the unfolding can be modeled as a random walk for its bond coordinate. A DFS experiment can be thought of as an activated escape of a brownian particle from a potential well, which accounts for all the intramolecular forces that hold the molecule in a particular configuration. The goal then is to infer the shape of the potential well from rupture time/force data.

Some relevant literature:

1. P.-W. Fok and T. Chou, Reconstruction of potential energy profiles from multiple rupture time distributions, Proceedings of the Royal Society A 466, No. 2124 pp 3479-3499 (2010)
2. Bal, G. and Chou, T., On the reconstruction of diffusions using a single first-exit time distribution. Inverse Problems 20, 1053-1065 (2003).
3. Dudko, O. K., Hummer, G. and Szabo, A., Theory, analysis, and interpretation of single-molecule force spectroscopy experiments. Proc Natl Acad Sci USA 105, 15755-15760 (2008).
4. Evans, E., Ritchie, K. and Merkel, R. Sensitive force technique to probe molecular adhesion and structural linkages at biological interfaces. Biophysical Journal 68, 2580-2587 (1995).
5. Freund, L. B. Characterizing the resistance generated by a molecular bond as it is forcibly separated. Proc Natl Acad Sci USA 106, 8818-8823 (2009).

Previous Research Projects

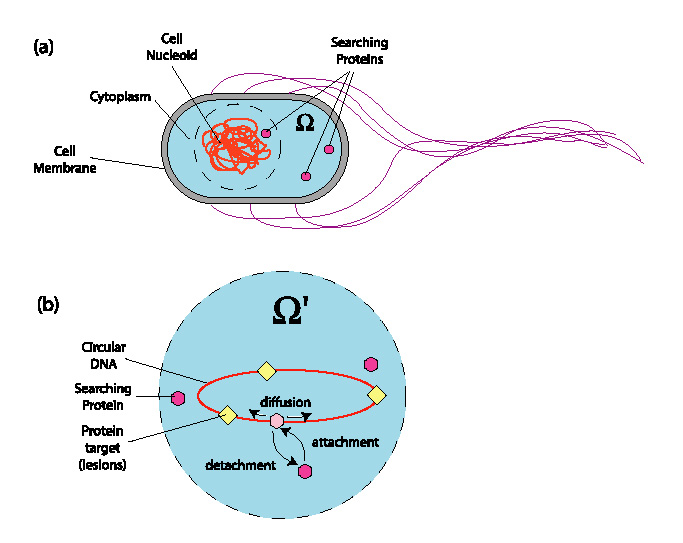
DNA repair enzymes are responsible for locating and repairing damaged bases on DNA. Without them, mutations in the DNA can occur, ultimately giving rise to diseases like cancer. An important problem that has puzzled biophysicists since the 70s is how enzymes are able to find small targets (such as damaged bases) on a long DNA strand so rapidly. For example the time to perform a 1D random search along a DNA strand, with the enzyme permanently associated with the DNA, is so long that it exceeds even the life cycle of the cell! Likewise, a 3D random search within the volume of a cell nucleus (or within the cell itself for prokaryotes) yields search times that are inconsistent with experimental reaction rates.

In the 1980s, a theory called facilitated diffusion was proposed to explain fast search times for searching enzymes. The theory posited that up to a 100 fold speed-up in the search could occur if a combination of 1D and 3D searches was used. However facilitated diffusion requires certain conditions to be met. For example, the enzyme must spend half the search time in 1D and half in 3D. These conditions are seldom met in practice. Subsequently many researchers have tried to refine and extend the theory to real biological systems.

Some relevant literature:

1. P.-W. Fok and T. Chou, Accelerated search kinetics mediated by redox reactions of DNA repair enzymes, Biophysical Journal 96, pp 2949-3958 (2009).
2. P.-W. Fok and T. Chou, Charge transport mediated recruitment of DNA repair enzymes. J. Chem. Phys. 129 235101 (2008).
3. O.G. Berg, R.B. Winter and P.H. Von Hippel, Diffusion-driven mechanism of protein translocation on nucleic acids. 1. Models and theory. Biochemistry 20 pp 6929-6948 (1981).
4. M. Slutsky and L. A. Mirny, Kinetics of protein-DNA interaction: facilitated target location in sequence-dependent potential. Biophysical Journal 87 pp 4021 - 4035 (2004).
5. T. A. Hu, A. Y. Grosberg and B. I. Shklovskii, How proteins search for their specific sites on DNA: the role of DNA conformation. Biophysical Journal 80 pp 2731-2744.

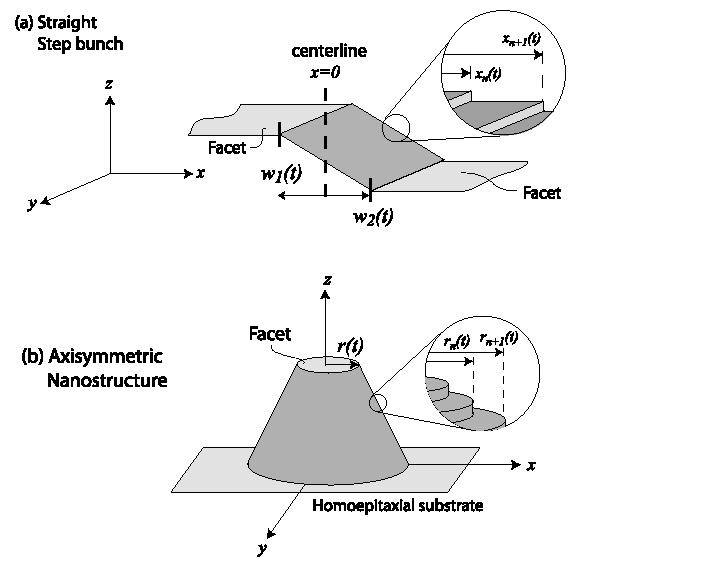
A vicinal surface is one that results from a slight miscut from a high symmetry plane of a crystal. As a result, the evolution of the surface is mediated by the motion of discrete atomic-height steps. These steps change their position in response to attachment-detachment kinetics at step edges and diffusion on terraces (the region between steps). For relaxing axisymmetric nanostructures under near-equilibrium conditions, the circular steps of these nanostructures are subject to two kinds of physical effect. First, the radii of steps shrink because of step line tension. Second, step-step repulsions (stemming from entropic and/or elastic interactions) ensure that steps cannot get too close to each other. As relaxation proceeds, a circular facet develops on the top of the structure and expands as the inner most steps repeatedly collapse.

It has been known for some time (e.g. see publication #4 below) that within a macroscopic treatment, nanostructure relaxation below the roughening temperature is described by nonlinear PDEs that are singular at facet edges. These singularities are intimately related to the non-analyticity of the surface free energy below the roughening temperature. One way to to solve these problems is to regard the facet edge as a free boundary whose position is time dependent and unknown a priori (see publication #3). The question that naturally arises is what the boundary conditions should be at the facet edge. In publication #1, we propose a boundary condition that depends on the motion of the inner most step: if the step collapse frequency is large, the facet expands quickly. On the other hand, if the inner most step does not move at all, the facet is frozen in time. The boundary condition bridges two length scales, coupling together the downward macroscopic translation of the facet with microscopic step collapses. Application of this boundary condition yields solutions that are in excellent agreement with simulation results.

In publication #2, we study finite and semi-infinite collections of straight and circular steps, comparing the discrete equations to their respective continuum PDEs. Boundary conditions are derived from simple physical considerations at the facet edges. For straight steps, simple similarity solutions exist which -- in some sense -- provide an exact description of the step motion. The solutions have different scalings in time depending on whether the system is semi-infinite or strictly finite. For circular steps where step-step interactions are weak compared to step line tension, the continuum PDE reduces to a kinematic wave equation. Shockwave theories and the method of characteristics can be used to treat facet translation in this case.

Some relevant literature

1. D. Margetis, P.-W. Fok, M.J. Aziz and H.A. Stone, Continuum theory of nanostructure decay via a microscale condition, Physical Review Letters 97, 096102 (2006)
2. P.-W. Fok, R. R. Rosales and D. Margetis, Facet evolution of supported nanostructures: Effect of finite height Physical Review B 78, 235401 (2008)
3. H. Spohn, Surface dynamics below the roughening transition, J. Phys. I France 3 pp 69-81 (1993)
4. A. Rettori and J. Villain, Flattening of grooves on a crystal surface: a method of investigation of surface roughness. J. Phys. France 49 pp 257-267 (1988)

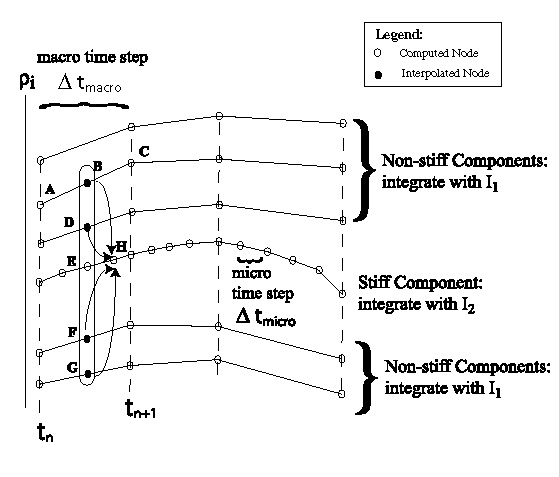
Multirate integration of a set of Ordinary Differential Equations (ODEs) involves taking time steps of different size for different components in the solution. This strategy is especially useful when a small fraction of the components evolves on faster time scales than the rest.

One of the main difficulties with implementing multirate methods is that slower components in the ODE system have to be interpolated accurately. Another difficulty is that it is unclear what order of interpolant is needed if the multirate method is to be of nth order. Can this interpolation be implemented without using any extra function evaluations from the ODE? Our group is currently developing a 4th order multirate method for locally coupled ODEs. Our aim is to apply this method to a wide variety of PDEs that have been discretized using the method of lines.

Some relevant literature

1. C.W. Gear and D.R. Wells, Multirate linear multistep methods, BIT 24 484 (1984).
2. A. Logg, Multi-adaptive time integration, Appl. Numer. Math 48 pp 339-354 (2004).
3. V. Savcenco, W. Hundsdorfer and J.G. Verwer, A multirate time stepping strategy for stiff ordinary differential equations, BIT 47 pp 137-155 (2007).
4. W. Hundsdorfer and V. Savcenco, Analysis of a multirate theta-method for stiff ODEs, Applied Numerical Mathematics 59 pp 693-706 (2008).