Marching Squares (Isolines) in Java

This code generates Java 2D GeneralPaths representing isolines of a data set. It is intended to be easy to use - please offer suggestions if you feel it is not. It is a direct implementation of the algorithm, not optimized for speed or efficiency, presented at the Wikipedia Marching Squares page. To the authors of that page, thank you!

Download

The code is distributed under the Free Software Foundation GNU Public License:

MarchingSquares.java, v0.1, Apr 22, 2013 (less efficient, easier to understand)
IsoCell.java, v0.3, May 12, 2021
Modified version: marchingSquares-v0.3.tar.gz, v0.3, Dec 17, 2014

History

MarchingSquares.java
2013-04-22: v0.1. Initial release.

IsoCell.java
2013-04-13: v0.1. Initial release.
2013-11-12: v0.2. Corrected error in starting subpath in IsoCell.firstSideCCW(). Thanks to Nicole Dröge whose careful testing located this error.
2021-05-12: v0.3. Corrected another error in starting subpath (case 11). Thanks to Giovanni Martino, who caught this one.

IsoCell can be inserted in MarchingSquares as a private inner class if desired.

N.B.: the java files above reference package 'map'. Be sure to change 'map' to your package name.

marchingsquares.tar.gz
2014-12-17: v0.3. Raif Naffah made substantial, practical improvements to the code. While my original code is mostly a one-for-one implementation of the algorithmic steps, Raif turned the code base into an efficient implementation. Excerpting his description,

I now have a solid implementation of this algorithm. By 'solid' I mean good performance and low memory usage.

The algorithm is now run in parallel; 1 thread per 1 isovalue.
The core of the algorithm is in the Algorithm.contour static method. The input is the padded 2D data value matrix and an isovalue, and the output is an instance of Grid: a DAO (data access object) that manages a sparse matrix of Cell instances. Only non-trivial contour cells (instances of Cell) are instantiated.
The bulk of the cell traversal logic is housed in the PathGenerator class. The main method (generate) takes a Grid instance and produces a GeneralPath.
In terms of accuracy, the code uses single-precision arithmetic. so EPSILON is only 1E-7 and all the side crossing coefficients are Java native floats.

Usage

There are four steps for usage:

Generate isolines.
Scale to world coordinates. (Permanent.)
Scale to screen coordinates. (Changes with pan/zoom.)
Draw isolines.

Variables in sections below are color coded to help tie together steps.

1. Generate Isolines

Sample usage:

    double[][] data_mW = .....; // create rectangular array of measured data.
    double[] levels_mW = .....; // create 1-D array of thresholds.

    MarchingSquares marchingSquares = new MarchingSquares();
    GeneralPath[] isolines = marchingSquares.mkIsos(data_mW, levels_mW); // <== Just this to create isos!

2. Scale to World Coordinates

For each threshold levels_mW[i], its corresponding iso is returned in isolines[i] whose coordinates are in units of array indices. If data_mW[][] is an m x n array, the isoline coordinates are indices into a padded array of size m+2 x n+2. The padding surrounds data with values lower than the lowest value in the set to guarantee that closed polygons are generated at image edges.

The isoline coordinates are now scaled into suitable units. For example, if the data was measured between lower left latitude and longitude of lat0/lon0 and upper right of lat1/lon1, and if it was binned into a cellsX by cellsY array, the following code positions and scales the isolines:

    // Convert isos from array coords to lat/lon coords.
    AffineTransform xf = new AffineTransform();
    xf.translate(lon0, lat0);
    xf.scale((lon1 - lon0) / (cellsX - 1), (lat1 - lat0) / (cellsY - 1));
    xf.translate(-1, -1); // Because MxN data was padded to (M+2)x(N+2).
    for (int i = 0; i < isolines.length; i++) {
        isolines[i].transform(xf); // Permanent mapping to world coords.
    }

3. Scale to Screen Coordinates

To pan and zoom, world coordinates are converted to screen coordinates. This is application specific, but once an AffineTransform xfDev is created that converts from world to screen coordinates it is used to map each isoshape to the screen.

    Shape iso = xfDev.createTransformedShape(isolines[level]); // Remapped every pan & zoom.

4. Draw Isolines

Drawing the isolines using Graphics2D variable g2 is easy:

    g2.setColor(isoColor);
    g2.fill(iso); // Color iso.
    g2.setColor(Color.gray);
    g2.draw(iso); // Outline iso.

Sample Output

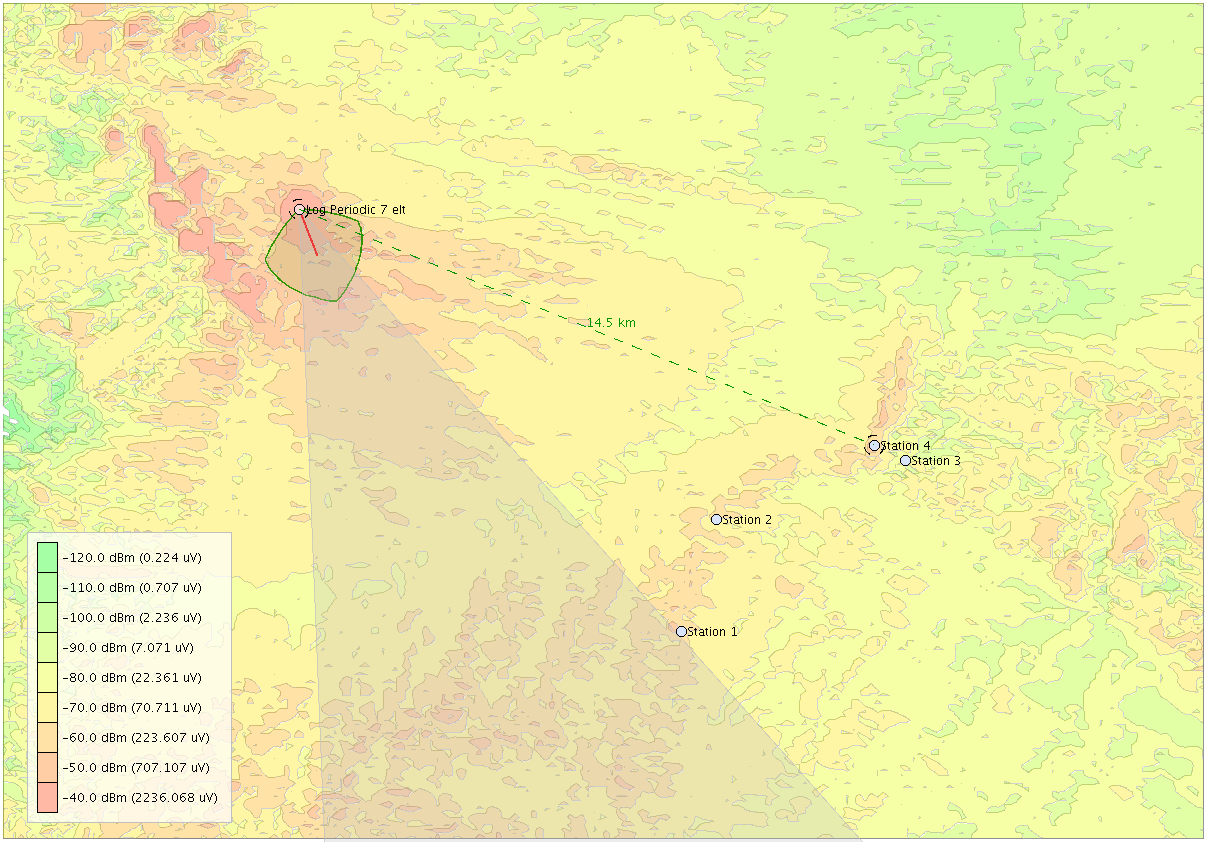
The snippets of code above are taken from an RF power coverage simulator that generated the map below. Notice the disjoint polygons and holes for a given threshold as implemented by GeneralPath.

5. Examples of Implementations

My area of research is RF propagation, but iso-lines and iso-surfaces are of course widely useful. If you find the code helpful I would be happy to receive screenshots of how you make use of it and add it to a gallery of examples. Please send me pictures of your application.

Examples are on this page.

I hope you find it useful and will notify me of any enhancements or bug fixes. I can imagine, for example, adding a filter to avoid creating polygons and holes that are less than a specified area. Where there are 'for' loops calculating transformations would be perfect places to use worker threads. No doubt there is room for optimization.

- Mike Markowski