DNA Slider is program for performing four significance tests of heterogeneity in the ratio of polymorphic sites to fixed differences in DNA sequence data. It is available for classic Macintosh, Mac OS X, and Windows. It performs the runs test described in:
McDonald, J.H. 1996. Detecting non-neutral heterogeneity across a region of DNA sequence in the ratio of polymorphism to divergence. Molecular Biology and Evolution 13:253-260,
and the mean sliding G-test, the maximum sliding G-test, and the Kolmogorov-Smirnov test described in:
McDonald, J.H. 1998. Improved tests for heterogeneity across a region of DNA sequence in the ratio of polymorphism to divergence. Molecular Biology and Evolution 15: 377-384.
The goal of the program is to identify genes that have more heterogeneity in the polymorphism-to-divergence ratio than expected under a neutral model. Peaks of high polymorphism may result from balancing selection, while areas of low polymorphism may be the result of selective sweeps.
The original (classic Mac OS) version of the program was written using the CodeWarrior Pascal compiler; it was ported to Mac OS X, Windows and Linux using the Free Pascal compiler. (Thanks to Andy Roosen for compiling the Linux version.) You can look at the DNA Slider source code, if you want. Free Pascal is available for several other operating systems, and because the new versions of DNA Slider use a simple console interface, it should be easy to compile it for other operating systems (or using other Pascal compilers, I imagine).
Download the appropriate version and put it in the same folder as your data files.
You may also want to download an example data set, data on the Acp26A region (formerly known as Mst26A) from Aguadé, M., N. Miyashita, and C.H. Langley. 1992. Polymorphism and divergence in the Mst26A male accessory gland gene region in Drosophila. Genetics 132:755-770. This data set is derived from 10 Drosophila melanogaster sequences and one D. simulans sequence, and it is 1557 nucleotides long.
The first step in using DNA Slider is to collect your data. You should have multiple DNA sequences from one species (the "polymorphism species") and one sequence from a closely related species (the "outgroup species"). The two species should be close enough that there are very few sites that have experienced multiple substitutions. If you have multiple sequences from the outgroup species, pick one of the sequences at random.
Align the sequences and identify all of the varying sites. Create an input file that has the name of the gene on the first line; the second line has the number of varying sites. The rest of the file consists of one line for each varying site, with the site number followed by a "P" or "F" for polymorphism or fixed difference.
The Windows-only program DnaSP will generate a DNA Slider input file from a set of aligned sequences; if you use a different program to look at aligned sequences, it's fairly easy to generate the list of polymorphisms and fixed differences by hand. Here's some imaginary data:
outgroup AATGCATCGAATCATTATGGC
allele 1 AACGCATCTAATCATCATGGC
allele 2 AACGCATCTAATGATGATGTC
allele 3 AACGCGTCTAATAATGATGCC
allele 4 AACGCGTCAAATAATAATGAC
3 6 9 1 1 2
3 6 0
Site 3 is a fixed difference between the outgroup species and the species with polymorphism data. Site 6 is a polymorphism. Most of your varying sites should be like these two, but you may have some more complicated sites. Site 9 has one fixed difference and one polymorphism. The fixed difference is the G that is in the outgroup species but not the polymorphism species; a mutation from G to A or T, or from A or T to G, must have occurred on the between-species part of the phylogenetic tree. An A to T or T to A mutation occurred on the within-species part of the tree, hence the one polymorphism. Site 13 has two polymorphisms, because two mutations (C to G and C to A) occurred on the within-species part of the tree. Site 16 has one fixed difference and two polymorphisms, and site 20 has three polymorphisms.
If you have any sites with more than one substitution, list each substitution on a separate line. If a site has both a fixed difference and a polymorphism, put them in the order that reduces the heterogeneity in the polymorphism to divergence ratio, to be conservative. The sample data above would produce this data set:
sample gene 12 3 F 6 P 9 P 9 F 13 P 13 P 16 P 16 P 16 F 20 P 20 P 20 P
The input file must be saved in plain text format, and you must put it in the same folder as the DNA Slider program.
The program first asks you for the names of the two species, then the number of sequences. It then asks you the length of the sequence, in nucleotides. This value does not need to be accurate, and if you have a very long sequence with a relatively small number of varying sites, it might be a good idea to enter a much smaller value for the sequence length. For example, if your data has 60 varying sites spread over 50,000 nucleotides of sequence, you'd be better off saying the sequence length is something like 2,000 nucleotides. The sequence would be divided up into 2,000 "blocks" for the purpose of coalescence and recombination; as long as there are many more blocks than there are varying sites, the simulations would give the same results as if you simulated 50,000 nucleotides, only much more quickly.
The program next asks you how many recombination parameters to try; you then enter the recombination parameters. The recombination parameter, R, is proportional to the number of recombination events per gene per generation. Under the neutral model, the maximum heterogeneity in the polymorphism-to-divergence ratio is seen with intermediate levels of recombination. To be conservative, I recommend trying a range of recombination parameters, such as 1, 2, 4, 8, 16..., and using the one that gives the largest P-values. The time that the simulations take goes up dramatically as you get to higher recombination values, so I recommend that you use 1...16, then only do 32, 64, ... if the P-values are still increasing (and are less than 0.05).
I recommend that you start with a very small number of replicates and time the run for the set of recombination parameters you want to try, so you can estimate how long a full set of replicates will run for.
When the program asks for the name of the input file, type the name, including the extension (.txt). The input file must be in the same folder as the DNA Slider program.
Once you have analyzed the data, the program gives you the option to plot a sliding window graph. The console graph is necessarily crude, but the saved numbers can be imported to a real graphing program.
Unlike most sliding window graphs, the windows are a fixed number of varying sites (polymorphisms + fixed differences), not a fixed number of nucleotides. For example, if you set the window size to 20, the program calculates the proportion of the first 20 varying sites that are polymorphisms, then the proportion of varying sites 2 through 21, etc. It also calculates the G-value for a 2x2 G-test comparing polymorphisms and fixed differences inside and outside the window. The P-value for each G-value is also reported; it is the proportion of replicate simulations that had a G-value that large, with the recombination value that produced the largest maximum G-value. This P-value is also calculated for each possible proportion of polymorphisms; the results can be used to plot horizontal lines on the graph corresponding to the P<0.05 critical values of the polymorphism proportion.
The program is limited to 200 sequences, 1000 polymorphisms, 1000 fixed differences, 20,000 nucleotide sites, and 100,000 replicate simulations. E-mail me (mcdonald@udel.edu) if you need me to re-compile the program with larger values for some of these; it'll only take me a few minutes.
Here is the output from an analysis of the example data set; I've added explanatory comments in red.
There are 23 runs in your data on Acp26A in D. melanogaster. The Kolmogorov-Smirnov statistic is 0.106490. A window of 52 variable sites produces the largest average sliding G value. For a window size of 52 the average sliding G value is 10.7670. A window of 51 variable sites produces the largest maximum sliding G value. For a window size of 51 the maximum sliding G value is 24.9373.
This part reports the four test statistics for your observed data.
Number of sequences from D. melanogaster: 10 Outgroup species: D. simulans Length of Acp26A in D. melanogaster: 1557 Number of polymorphisms: 21 Number of fixed differences: 48 Number of replicate simulations: 5000 Recomb. max G >= runs <= K-S >= avg. G >= parameter 24.9373 23 0.106490 10.7670 1.00 0.0018 0.0380 0.0040 0.0000 2.00 0.0020 0.0380 0.0038 0.0006 4.00 0.0026 0.0490 0.0068 0.0000 8.00 0.0032 0.0492 0.0070 0.0002 16.00 0.0020 0.0554 0.0068 0.0000 32.00 0.0016 0.0604 0.0044 0.0000
This shows, for each value of the recombination parameter, the proportion of the simulated data sets that have a test statistic more extreme than the observed one. (A smaller number of runs is more extreme; a larger value of the other three statistics is more extreme.) As you can see, the P-values get larger as the recombination parameter increases, then start to go down with R=16, so it's not necessary to try higher recombination parameters. With other data sets, the R-value with the maximum P-values may be different.
Recomb. Maximum G critical values parameter P<0.05 P<0.01 1.00 14.4 19.0 2.00 14.8 20.2 4.00 15.7 21.4 8.00 16.2 21.1 16.00 16.3 20.6 32.00 15.7 20.2
This shows the P=0.05 and P=0.01 critical values of the maximum sliding G statistic.
===========Sliding window of 51 variable sites.========
Start Midpoint End prop. poly. G-value P-value
1 -22 566.5 1155 0.196 10.263 0.221000
2 -16 573.5 1163 0.176 14.355 0.092400
3 1 582.5 1164 0.176 14.355 0.092400
4 37 601.5 1166 0.157 19.219 0.014800
5 40 617.0 1194 0.157 19.219 0.014800
6 52 645.5 1239 0.157 19.219 0.014800
7 68 664.0 1260 0.137 24.937 0.001600
8 77 692.5 1308 0.157 19.219 0.014800
9 109 746.0 1383 0.176 14.355 0.092400
10 183 800.5 1418 0.176 14.355 0.092400
11 207 814.0 1421 0.196 10.263 0.221000
12 225 858.0 1491 0.216 6.889 0.497000
13 228 863.5 1499 0.235 4.198 0.797600
14 270 886.5 1503 0.255 2.170 0.987600
15 348 936.0 1524 0.235 4.198 0.797600
16 360 946.5 1533 0.255 2.170 0.987600
17 399 978.0 1557 0.275 0.800 1.000000
18 405 988.5 1572 0.294 0.096 1.000000
19 414 996.0 1578 0.314 0.082 1.000000
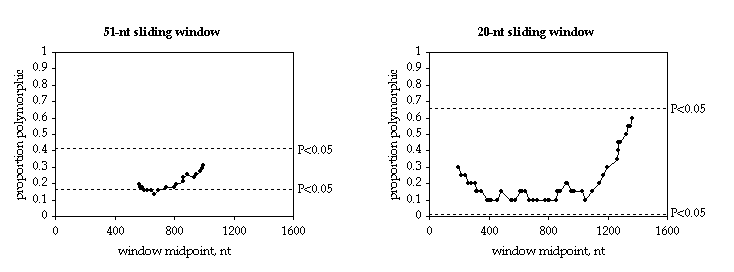
The numbers above are saved if you choose to graph your data. The proportion of varying sites that are polymorphic ("prop. poly.") and the midpoint of the sliding window can be used to plot a sliding window graph. These numbers are for a sliding window of 51 nucleotides, which produces the largest maximum sliding G value.
All possible G-values and P-values for a window of 51 variable sites.
prop. poly. G-value P-value
0.000 108.618 0.000000
0.020 90.733 0.000000
0.039 75.762 0.000000
0.059 61.982 0.000000
0.078 49.035 0.000000
0.098 39.527 0.000000
0.118 31.636 0.000000
0.137 24.937 0.001600
0.157 19.219 0.014800
0.176 14.355 0.092400
0.196 10.263 0.221000
0.216 6.889 0.497000
0.235 4.198 0.797600
0.255 2.170 0.987600
0.275 0.800 1.000000
0.294 0.096 1.000000
0.314 0.082 1.000000
0.333 0.808 1.000000
0.353 2.358 0.973800
0.373 4.893 0.726000
0.392 8.768 0.302400
0.412 15.697 0.056800
0.431 22.900 0.002800
0.451 30.367 0.000000
0.471 38.094 0.000000
.
.
.
The numbers above show, for each possible value of the polymorphism proportion for the chosen window size, the P-value (proportion of replicate simulations with a maximum G-value that large or larger). These numbers can be used to plot critical values on a sliding window graph; for example, the lower P<0.05 critical value for the above data is between 15.7 and 17.6 percent polymorphic, and the upper critical value is between 41.2 and 43.1 percent.
===========Sliding window of 20 variable sites.========
Start Midpoint End prop. poly. G-value P-value
1 -22 197.5 417 0.300 0.003 1.000000
2 -16 214.0 444 0.250 0.402 1.000000
3 1 239.5 478 0.250 0.402 1.000000
4 37 259.0 481 0.200 1.523 0.999600
5 40 282.5 525 0.200 1.523 0.999600
6 52 308.0 564 0.200 1.523 0.999600
7 68 319.0 570 0.150 3.455 0.879800
8 77 325.0 573 0.150 3.455 0.879800
9 109 351.5 594 0.150 3.455 0.879800
10 183 391.5 600 0.100 6.360 0.550400
11 207 406.5 606 0.100 6.360 0.550400
12 225 417.0 609 0.100 6.360 0.550400
13 228 459.0 690 0.100 6.360 0.550400
14 270 481.5 693 0.150 3.455 0.879800
15 348 549.0 750 0.100 6.360 0.550400
16 360 556.5 753 0.100 6.360 0.550400
17 399 579.0 759 0.100 6.360 0.550400
18 405 609.0 813 0.150 3.455 0.879800
19 414 627.0 840 0.150 3.455 0.879800
20 417 648.0 879 0.150 3.455 0.879800
21 444 675.0 906 0.100 6.360 0.550400
22 478 698.0 918 0.100 6.360 0.550400
23 481 727.0 973 0.100 6.360 0.550400
24 525 781.5 1038 0.100 6.360 0.550400
25 564 803.0 1042 0.100 6.360 0.550400
26 570 806.5 1043 0.100 6.360 0.550400
27 573 810.0 1047 0.100 6.360 0.550400
28 594 856.0 1118 0.100 6.360 0.550400
29 600 860.0 1120 0.150 3.455 0.879800
30 606 869.0 1132 0.150 3.455 0.879800
31 609 878.0 1147 0.150 3.455 0.879800
32 690 922.5 1155 0.200 1.523 0.999600
33 693 928.0 1163 0.200 1.523 0.999600
34 750 957.0 1164 0.150 3.455 0.879800
35 753 959.5 1166 0.150 3.455 0.879800
36 759 976.5 1194 0.150 3.455 0.879800
37 813 1026.0 1239 0.150 3.455 0.879800
38 840 1050.0 1260 0.100 6.360 0.550400
39 879 1093.5 1308 0.150 3.455 0.879800
40 906 1144.5 1383 0.200 1.523 0.999600
41 918 1168.0 1418 0.250 0.402 1.000000
42 973 1197.0 1421 0.300 0.003 1.000000
43 1038 1264.5 1491 0.350 0.273 1.000000
44 1042 1270.5 1499 0.400 1.185 0.999800
45 1043 1273.0 1503 0.450 2.723 0.963200
46 1047 1285.5 1524 0.450 2.723 0.963200
47 1118 1325.5 1533 0.500 4.887 0.726000
48 1120 1338.5 1557 0.550 7.687 0.446200
49 1132 1352.0 1572 0.550 7.687 0.446200
50 1147 1362.5 1578 0.600 11.143 0.177200
The 51-nucleotide sliding window, for a data set with only 69 varying sites, does not give a good view of the distribution of polymorphism. A 20-nucleotide window gives a more detailed view.
All possible G-values and P-values for a window of 20 variable sites. prop. poly. G-value P-value 0.000 17.876 0.025200 0.050 10.595 0.201400 0.100 6.360 0.550400 0.150 3.455 0.879800 0.200 1.523 0.999600 0.250 0.402 1.000000 0.300 0.003 1.000000 0.350 0.273 1.000000 0.400 1.185 0.999800 0.450 2.723 0.963200 0.500 4.887 0.726000 0.550 7.687 0.446200 0.600 11.143 0.177200 0.650 15.289 0.066000 0.700 20.175 0.010000 0.750 25.874 0.001400 0.800 32.490 0.000000 0.850 40.185 0.000000 0.900 49.226 0.000000 0.950 60.149 0.000000 1.000 75.038 0.000000
The numbers can be imported into a graphing program and used to create graphs like this:
Go back to John McDonald's home page
Send comments to mcdonald@udel.edu
Last Updated: February 22, 2015.
URL of this document: http://udel.edu/~mcdonald/aboutdnaslider.html